The Henderson-Hasselbalch Equation In Action On The MCAT
Consider the following problem: we mix nitrous acid, which has a Ka of 4.0 × 10-4, with its conjugate base at a 4:1 acid-base ratio. What is the pH of the resulting buffer solution? This simple-sounding problem contains several useful teaching points for handling acid-base chemistry with no calculator.
In this blog post, we’ll work through the problem systematically, drawing attention to some key “tricks” that you can apply to solve it, and then discuss how you can use these tricks to set yourself up for success on the MCAT chemistry questions.
Setting Up The Problem
The first thing to figure out for this question is how to approach solving it. As soon as you see that the question is asking about the ratio of a weak acid to its conjugate base, you should immediately think of the Henderson-Hasselbalch equation, which relates pH, pKa, and the ratio of [HA] (an acid) to [A–] (its conjugate base) as follows:
pH = pKa + log[A–]/[HA]
Calculating The pKa
This question gives us the acid-base ratio and the Ka, so our first task is to translate that information into the form we need for the Henderson-Hasselbalch equation. The first issue we need to deal with is going from Ka to pKa. Recall that in acid-base chemistry, pX means –log[X]: pH = –log{H+], pOH = –log[OH–], and so on. Therefore, to calculate the pKa, we need to calculate –logKa, which is –log(4.0 × 10-4), based on the information in the question. This may seem like a daunting mathematical task, but there’s a neat trick we can use to estimate this, given a value in scientific notation of N × 10-M:
p(N × 10-M) = (M-1).(10-N)
Let’s walk through this trick a little bit more carefully to see how it works. Since a logarithm in general corresponds to the power of 10, M will be the most important number for calculating the magnitude of the pKa value. We can use the question information to see this. If the Ka was 1.0 × 10-4, the pKa would just be 4, based on a straightforward definition of what a negative log is. If the Ka was 1.0 × 10-3 (which equals 10 × 10-4), the pKa would be 3. In this problem, we’re given a Ka of 4.0 × 10-4, which is somewhere between 1.0 × 10-4 and 1.0 × 10-3, so the pKa must be somewhere between 3 and 4.That’s what the (M-1) term in our shortcut means.
The next question is where does the pKa lie in that interval: is it closer to 3 or to 4? This of course depends on whether the Ka is closer to 1.0 × 10-4 or 1.0 × 10-3, and it turns out that we can get a good enough approximation just by subtracting the digit term (that is, the number before the × in scientific notation) from 10 and using that as the value after the decimal point. It’s worth taking the time to familiarize yourself with this trick, because this is a high-yield skill for MCAT math.
Using this trick, we can estimate the pKa of nitrous acid to be 3.6. If you do it with a calculator, you’ll find that the actual value is 3.4. This margin of error is close enough for the MCAT.
Estimating The pH
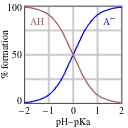
Now we need to tackle the acid-base ratio term. Before we do any math, though, let’s set expectations about the answer based on the passage information. Remember that the pKa corresponds, by definition, to the pH where a weak acid is half protonated and half deprotonated (that is, where [A–] = [HA]). If we reduce the pH, the solution will become more acidic and HA will predominate. If we increase the pH, in contrast, the solution will become less acidic, and the deprotonated form (A–) will predominate, as shown in the diagram below.
Since the passage tells us that there’s a 4:1 acid-base ratio, or in plain English that there is 4 times as much of the acid as there is of its conjugate base, we can automatically conclude that the pH must be lower than the pKa! At this point, we can eliminate any answer choices that are not lower than the pKa.
However, the question may give us two answer choices that are lower than the pKa, so we may have to determine how much lower the pH is. We can calculate this, but we should also use some general estimation techniques to minimize the math that we have to do. Recall that in the Henderson-Hasselbalch equation, we deal with the log of the ratio of [A–]/[HA]. This means that each increment of a power of 10 in the ratio will correspond to an increment of a single digit in the log of the ratio – so a 10x [A–]/[HA] ratio would correspond to a value of 1 for that term, a 100x [A–]/[HA] ratio would correspond to a value of 2, a 1000x [A–]/[HA] ratio would correspond to a power of 3, and so on. We’re told that the ratio is 4:1 in favor of the acid, so the [A–]/[HA] ratio is 1:4. This is less than a power of 10, so that means that we are looking for a pH that is lower than the pKa by less than 1 – or, in other words, a pH between 2.6 and 3.6. There will almost certainly only be one answer choice that fits the bill.
Reflecting On The Problem
Let’s step back and summarize what we did here: (1) we recognized the equation we needed to use, (2) we used a shortcut to calculate the pKa, (3) we used general reasoning about the scenario posed in the question to conclude that pH < pKa, allowing us to eliminate answer choices, and finally (4) we used our knowledge of how logarithms work to estimate the pH range we’re looking for—all without any precise calculations!
It’s particularly worth noting that we could have used this problem-solving technique even if we forgot key details about the Henderson-Hasselbalch equation, like whether a + sign or a – sign comes after the pKa, or whether it uses log[A–]/[HA] or log[HA]/[A–]. This is because we didn’t just memorize the equation – instead, we used our understanding of acid-base chemistry to make predictions.
Summing Up
In general, for MCAT chemistry, and for MCAT math in general, it’s a good idea to use shortcuts and estimations in your calculations and to be able to think through what a reasonable answer to the problem will be, for several reasons:
- To eliminate incorrect choices
- To ensure that you do the least work possible to get the right answer
- To serve as a reality check in case you make a silly mistake
Make sure you’re fully prepared for the MCAT exam. If you’re struggling with concepts like this or with other topics and sections, you should consider expanding your MCAT prep. Blueprint MCAT (formerly Next Step Test Prep) provides a Free MCAT Practice Bundle with plenty of resources to help you get started.
If you feel you need more help, we also provide guided prep options like our One-on-One Tutoring Programs and our comprehensive Online MCAT Course. Not sure what prep option is right for you? You can set up a free, no obligation consultation with one of our veteran Academic Managers. They can discuss your previous prep, your struggles, and your prep options. It can be a helpful conversation even if you don’t choose to work with us.
Good luck with your MCAT prep!
Written by Blueprint MCAT (formerly Next Step Test Prep) MCAT experts.
