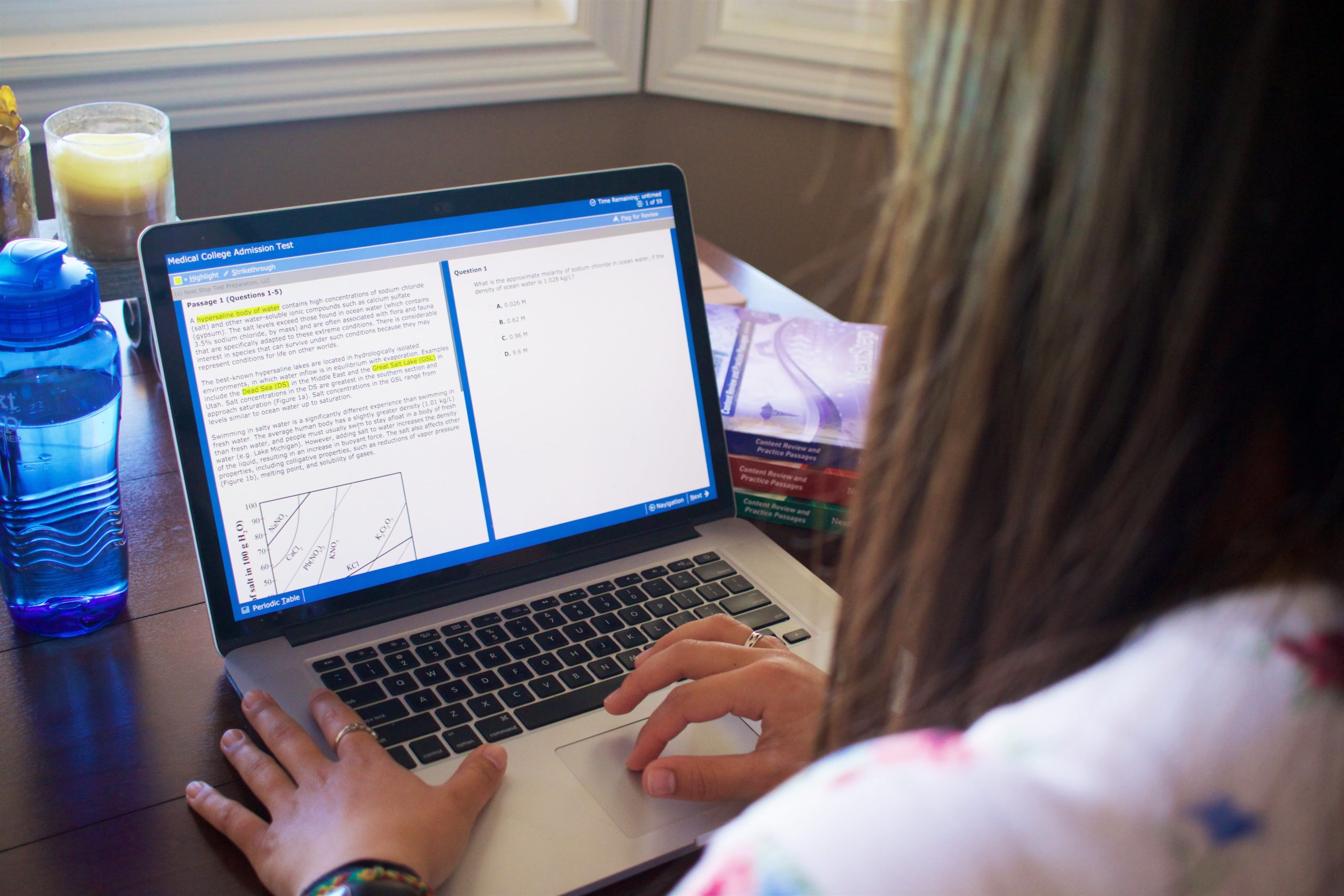
BLUEPRINT MCAT® BLOG
At Blueprint, we believe in educating first. Our MCAT blog was created to reflect this value. Our articles are written by the same MCAT experts who write our MCAT books, MCAT practice exams, and our MCAT course materials. We also partner with guest contributors regularly, both professionals and industry experts, to make sure that you are getting information that is not only relevant, but accurate.
Learn from the best with this free MCAT resource, updated with new articles regularly. If you need to know about a specific MCAT subject, changes being made to the MCAT exam, and general information about the MCAT, our blog is the perfect place for you.

Understanding the Difference Between Top-Down and Bottom-Up Processing for the MCAT
Discover the difference between bottom-up and top-down processing and how to incorporate both into your MCAT prep.
READ MORE
Everything You Need To Know about Amino Acids for the MCAT
There are few guarantees for what content might pop up on your MCAT, but I know one thing for certain: you will see amino acids on MCAT test day. Amino acids are the fundamental building blocks of proteins and mastering the properties, structures, and functions of amino acids is essential for success on the MCAT
READ MORE
Do You Need Research Experience for Medical School?
Do you need research experience for medical school? Find out if it's a requirement, how many hours you need, and where to find opportunities.
READ MORE
The Ultimate 6-Month MCAT Study Schedule
So you're taking the MCAT, but you're not sure what a study plan even looks like. Check out this high-level outline and find out how you can create a free MCAT study plan with Blueprint MCAT!
READ MORE
Essential MCAT Equations To Memorize
Discover essential MCAT equations to memorize for effective MCAT preparation.
READ MORE
Medical Schools Offering Full-Tuition Scholarships
Looking for scholarships for medical school? Explore these medical schools that offer awesome full-tuition scholarships!
READ MORE
How To Maximize the Last Semester of Your Premed Senior Year
Discover how to rock your second semester of senior year to finish strong and gear up for success in the medical school admissions journey.
READ MORE
MCAT Diaries: Losing and Rediscovering My Passion for Medicine
Do you ever feel like maybe medical school isn't in the cards for you? Read about how this former Blueprint MCAT student rediscovered thei passion for medicine.
READ MORESearch the Blog

Free Consultation
Interested in our Online MCAT Course, One-on-One MCAT Tutoring or Med admissions packages? Set up a free consultation with one of our experienced Senior Student Advisors.
Schedule NowPopular Posts
-
MCAT Blog What's on the MCAT?
-
MCAT Blog How to Review MCAT Full Lengths

Free MCAT Practice Account
Need great MCAT practice?Get the most representative MCAT practice possible when you sign up for our free MCAT Account, which includes a half-length diagnostic exam and one of our full-length MCAT practice exams.
Learn More